Quand obtenir une plus grande résolution avec la technique du drizzle
Le drizzling, pour des images de plus grande résolution
Hubble connaît également ce problème : comment arrive-t-on à un sous-échantillonnage et quel logiciel aide à résoudre le problème ?
 L’amas globulaire M5 : à gauche, avec empilement normal. À droite, avec drizzle-stacking de 20 images, temps d’exposition 300 s chacune. Pour comparaison, la version normale a été mise à la même échelle d’image que l’image reconstruite. Le setup, pour l’image, se situait dans la plage de sous-échantillonnage, reconnaissable aux nombreux profils d’étoiles reproduits de façon non idéale et apparaissant quelque peu pixelisés. Une lunette avec une ouverture de 105 mm et une distance focale de 670 mm était équipée d’un appareil photo avec des pixels de 9 µm. L’échantillonnage se situe ainsi à 2,77"/pixel, pour un pouvoir de résolution théorique de 1,14". La technique du drizzle permet une résolution plus fine des étoiles fortement groupées et les couples d’étoiles rapprochées sont plus nettement séparés (résultat à droite). M. Weigand
L’amas globulaire M5 : à gauche, avec empilement normal. À droite, avec drizzle-stacking de 20 images, temps d’exposition 300 s chacune. Pour comparaison, la version normale a été mise à la même échelle d’image que l’image reconstruite. Le setup, pour l’image, se situait dans la plage de sous-échantillonnage, reconnaissable aux nombreux profils d’étoiles reproduits de façon non idéale et apparaissant quelque peu pixelisés. Une lunette avec une ouverture de 105 mm et une distance focale de 670 mm était équipée d’un appareil photo avec des pixels de 9 µm. L’échantillonnage se situe ainsi à 2,77"/pixel, pour un pouvoir de résolution théorique de 1,14". La technique du drizzle permet une résolution plus fine des étoiles fortement groupées et les couples d’étoiles rapprochées sont plus nettement séparés (résultat à droite). M. WeigandSi l’on utilise un capteur grand format pour photographier une grande zone du ciel, il peut en résulter un sous-échantillonnage, problème qui concerne également le télescope spatial Hubble. Une méthode astucieuse pourrait y remédier : la technique du drizzle.
La résolution des détails d’une image est déterminée par les conditions d’observation, mais aussi par deux facteurs côté instrument : le pouvoir de résolution du télescope et la finesse de la matrice de pixels de l’appareil photo. Les combinaisons appareil photo/télescope n’exploitent pas toutes entièrement le pouvoir de résolution de l’optique. Si l’on choisit par exemple un capteur grand format avec des pixels relativement grands, pour photographier une zone du ciel aussi grande que possible, on se heurte à un sous-échantillonnage. Le télescope Hubble, avec la « caméra planétaire à grand champ », se trouve lui aussi dans cette situation, ce qui fait qu’un algorithme a été développé pour récupérer une partie du pouvoir de résolution perdu : la technique du drizzle.
L’idée à la base de la technique du drizzle développée par A. Fruchter et R. Hook est l’utilisation de plusieurs images, où la matrice de pixels, trop grossière, est légèrement décalée d’une image à l’autre par rapport à l’objet. Ce décalage permet de détecter l’objet dans la plage des sous-pixels.
À ces fins, les pixels de toutes les images sont réduits et projetés sur une matrice de pixels plus fine. En fonction du chevauchement des deux matrices de pixels, les valeurs de luminosité se diffusent (drizzle) et sont redistribuées sur la nouvelle matrice. Pour la nouvelle matrice, les valeurs de luminosité de toutes les images d’une série sont moyennées, pour chaque pixel. Si l’on choisit un facteur de drizzle faible, on obtient une représentation régulière, avec un échantillonnage plus fin, lorsque l’on empile de nombreuses images.
Dithering et images multiples
Le léger décalage entre les différentes images d’une série, nécessaire pour la méthode du drizzle, peut être généré par dithering. La position du télescope est alors automatiquement et aléatoirement décalée de quelques pixels après chaque prise de vues. Le dithering est de toute façon la plupart du temps utilisé pour éliminer les pixels perturbateurs par une méthode d’empilement appropriée. On peut le faire, par exemple, via l’autoguider qui suit une position décalée de quelques pixels après chaque prise de vues. Tous les logiciels d’autoguidage courants offrent cette option.
Il faut en outre autant d’images que possible pour reconstituer les informations perdues. Ce n’est qu’alors que l’on peut combler les vides qui se créent lors de la redistribution des valeurs de luminosité.
 La même étoile, sur différentes images, entre lesquelles la position a été légèrement modifiée. Le profil de l’étoile apparaît asymétrique, ce à quoi on reconnaît le sous-échantillonnage. En outre, le changement de profil d’image en image, est utilisé par l'algorithme Drizzle. M. Weigand
La même étoile, sur différentes images, entre lesquelles la position a été légèrement modifiée. Le profil de l’étoile apparaît asymétrique, ce à quoi on reconnaît le sous-échantillonnage. En outre, le changement de profil d’image en image, est utilisé par l'algorithme Drizzle. M. WeigandLimites de la méthode
Naturellement, la technique du drizzle a aussi ses limites. Le facteur de drizzle n’est pas arbitraire car l’échantillonnage ne peut pas être augmenté à volonté. Le nombre d’images nécessaires pour une représentation uniforme serait très important et pratiquement irréalisable. Un facteur de 2 est en général recommandé. En outre, la technique est limitée par le pouvoir de résolution du télescope et par le seeing. Avec le seeing typique en Allemagne, la technique du drizzle devrait rarement être bénéfique pour les longs temps d’exposition avec un échantillonnage d’environ 1,5"/pixel ou plus fin. Cette technique est surtout intéressante pour les situations de sous-échantillonnage, par exemple les prises de vues d’ensemble de la Lune et du soleil, de même que dans la zone du ciel profond à des distances focales plutôt courtes. Il est également à noter que la technique du drizzle ne peut pas être combinée à des méthodes d’empilement comme l’empilement médian ou l’empilement sigma. Les pixels de la matrice plus fine ne sont en effet alimentés en contenu que par alternance, ce qui équivaut à l’apparition d’un pixel perturbateur qui est mis de côté lors de ces processus d’empilement.
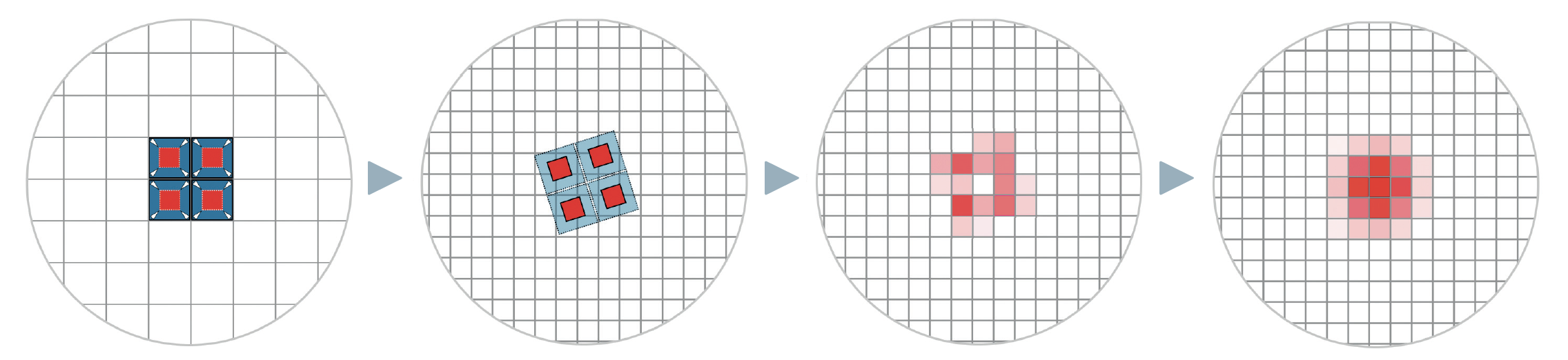 Concernant le principe de fonctionnement de la technique du drizzle : sur l’image gauche, une étoile est placée exactement à l’intersection de quatre pixels et ses valeurs de luminosité se répartissent régulièrement entre les pixels. L’étoile apparaît ainsi pixelisée et son profil à proprement parler n’est pas reproduit. La matrice de pixels originale de l’image (bleue) est alors réduite (rouge) et projetée sur une nouvelle matrice (deuxième image). La nouvelle matrice est ici plus fine à concurrence du facteur 2. Avec une image seulement, on obtient naturellement des vides en certains endroits, comme on peut le voir dans la répartition des valeurs qui en résulte, sur la troisième image. C’est pourquoi de nombreuses images avec des décalages faibles et variables sont nécessaires. Après établissement de leur moyenne, le profil d’étoile n’est mieux représenté que dans le cas idéal (image à droite). M. Weigand
Concernant le principe de fonctionnement de la technique du drizzle : sur l’image gauche, une étoile est placée exactement à l’intersection de quatre pixels et ses valeurs de luminosité se répartissent régulièrement entre les pixels. L’étoile apparaît ainsi pixelisée et son profil à proprement parler n’est pas reproduit. La matrice de pixels originale de l’image (bleue) est alors réduite (rouge) et projetée sur une nouvelle matrice (deuxième image). La nouvelle matrice est ici plus fine à concurrence du facteur 2. Avec une image seulement, on obtient naturellement des vides en certains endroits, comme on peut le voir dans la répartition des valeurs qui en résulte, sur la troisième image. C’est pourquoi de nombreuses images avec des décalages faibles et variables sont nécessaires. Après établissement de leur moyenne, le profil d’étoile n’est mieux représenté que dans le cas idéal (image à droite). M. WeigandLogiciel
Malheureusement, seuls certains logiciels d’empilement offrent une option drizzle ou un algorithme similaire. Pour des vidéos d’objets du système solaire, on trouve la fonction dans les logiciels AutoStakkert! et RegiStax, par exemple. Pour les images du ciel profond, on peut également citer Fitswork et DeepSky-Stacker. Tous ces logiciels sont disponibles gratuitement sur Internet.
Conclusion
Drizzle permet de mieux exploiter le pouvoir de résolution d’un télescope face à un sous-échantillonnage donné et d’améliorer la définition des profils d’étoiles. Il en résulte des avantages en ce qui concerne la restitution des détails. La méthode fonctionne si les conditions suivantes sont remplies : la combinaison appareil photo/télescope se trouve dans la zone de sous-échantillonnage, on dispose du plus grand nombre possible d’images individuelles et il y a un décalage entre celles-ci (dithering).
Auteur : Mario Weigand / Licence : Oculum-Verlag GmbH
